Spielen. Spielen macht Spaß. Spielen entspannt. Spielen verbindet. Zumindest so lange, bis sich Mathematiker daran machen, die Mechanik eines Spiels in komplexen Modellen und Formelsprache abzubilden. Die Spieltheorie ist eine Ernst zu nehmende Teil-Disziplin in der Mathematik. Dabei geht es nicht nur darum zu untersuchen, wie man stets als Sieger aus einem Spiel hervorgeht. Es geht vor allem darum, unterschiedliche Strategien in ihrer Erfolgswahrscheinlichkeit zu vergleichen. Was passiert, wenn man auf eine spezielle Weise, d.h. nach einer definierten Strategie spielt? Was, wenn man das Gegenteil tut? Mit Computerhilfe kann man heute x-beliebige Strategien ausprobieren, selbst wenn diese theoretisch überhaupt nicht erfolgversprechend sind. Dabei kann man manche Überraschung erleben. Am Beispiel des berühmt-berüchtigten „Gefangenendilemmas“ führt Gerrit erst einmal in die Grundlagen der Spieltheorie ein. Kurz bevor unsere Köpfe explodieren, gehen wir dann zum konkreten Artikel über, wo uns die Überraschung erwartet, dass sich – bei geeigneter Wahl der Strategie – das Spielergebnis des Gegners aktiv beeinflussen lässt. Und es ist dabei ganz egal, was der Gegner tut. Er ist immer „Spielball“ unserer Strategie und sein Gewinn wird vorhersagbar. Natürlich stellt sich die Frage, ob sich solche Spielvarianten auch auf das allgemeine Alltagsleben übertragen lassen. Das geht nicht 1:1, doch gewisse Parallelen lassen sich, bei aller gebotenen Vorsicht, dann doch herbeiphilosophieren. Für größere Populationen ergibt sich außerdem die paradoxe Situation, dass der bewusste Verzicht auf einen sicheren Sieg langfristig die erfolgreichere Strategie zu sein scheint.
Aufnahme vom 14.04.2015 – Dauer: 2:32:41
Links:
Spieltheorie – Gefangenendilemma mit Erpressung (Brian Hayes)
http://www.spektrum.de/alias/spieltheorie/gefangenendilemma-mit-erpressung/1313485
(Iteriertes) Gefangenendilemma
http://de.wikipedia.org/wiki/Gefangenendilemma
Spieltheorie, Rationale Spieler
http://de.wikipedia.org/wiki/Spieltheorie
Gewinnstrategie
http://de.wikipedia.org/wiki/Strategie_%28Spieltheorie%29
Gesellschaftsspiele
http://de.wikipedia.org/wiki/Gesellschaftsspiel
Roulette
http://de.wikipedia.org/wiki/Roulette
Tic Tac Toe
http://de.wikipedia.org/wiki/Tic_Tac_Toe
Homo Ökonomikus
http://de.wikipedia.org/wiki/Homo_oeconomicus
Gemischte Strategien
http://de.wikipedia.org/wiki/Gemischte_Strategie
John Nash
http://de.wikipedia.org/wiki/John_Forbes_Nash_Jr.
Nash Gleichgewicht
http://de.wikipedia.org/wiki/Nash-Gleichgewicht
A Beautiful Mind – Genie und Wahnsinn
http://de.wikipedia.org/wiki/A_Beautiful_Mind_%E2%80%93_Genie_und_Wahnsinn
Nullsummenspiel
http://de.wikipedia.org/wiki/Nullsummenspiel
John von Neumann
http://de.wikipedia.org/wiki/John_von_Neumann
Minimax-Theorem
http://de.wikipedia.org/wiki/Min-Max-Theorem
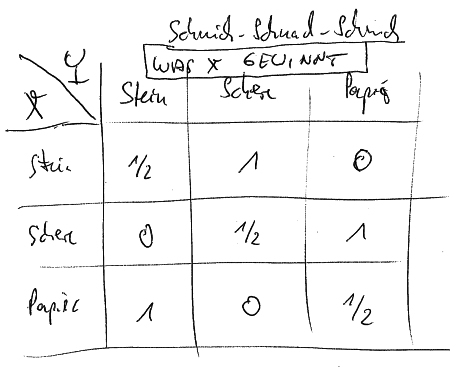
Schnick, Schnack, Schnuck | Schere, Stein Papier
http://de.wikipedia.org/wiki/Schere,_Stein,_Papier
Scissors, Paper, Stone – unbeatable robot wins every hand
https://www.youtube.com/watch?v=IfNTulf1zRs
Schere schneidet Papier / Papier bedeckt Stein / Stein zerquetscht Echse / Echse vergiftet Spock / Spock zertrümmert Schere / Schere köpft Echse / Echse frisst Papier / Papier widerlegt Spock / Spock verdampft Stein / Stein schleift Schere
https://twitter.com/scifunkel/status/589006512187691008
Berühmte Probleme: Kampf der Geschlechter
http://de.wikipedia.org/wiki/Kampf_der_Geschlechter
Instinkt
http://de.wikipedia.org/wiki/Instinkt
Rheinischer Kapitalismus
http://de.wikipedia.org/wiki/Rheinischer_Kapitalismus
@Planet_Kai ich habe einen Quarter aus New Mexico. Zum Werfen, falls die Münze eine Entscheidung treffen soll :)
— yvonne (@piratte) 17. April 2015